Introduction

Consider the following steps in a basic algebra problem:

Solve for x:

x + 3 = 5
x = 5 - 3
x = 2

Now suppose two different students have learned how to solve problems such as the one above and they now encounter a new situation:

Solve for x:

4x = 16

Let us further suppose that our students have never seen a problem involving multiplication of algebraic variables. The students think out loud as they try to solve this problem. Here is what they might say:

Student 1:  "I want to solve for x, so I need to get x by itself. In order to maintain the equality as before, I must do the same thing to both sides of the equation. I can isolate x if I multiply 4x by 1/4, so that's what I'll do to both sides of the equation."

(1/4)(4x) = (1/4)(16)
x = (1/4)(16)
x = 4

Student 2:  "I need to get x by itself again. In the previous problems, I took the number to the other side and made it negative, so I'll do that again."

x = 16 - 4
x = 12

Which of the two students would you say understands the concepts associated with solving linear equations? Which student has memorized a set of procedures or algorithms? If you said that student 1 understands the concepts, you are in agreement with most cognitive psychologists who study how people solve problems. Student 1 is able to successfully apply the concepts in a novel situation, which is an indication that the student understands the concepts. Unfamiliar problems that require previously-encountered concepts for their solution are "transfer problems."

Conceptual understanding is superior to memorized algorithms for solving transfer problems (Katona, 1940; Mayer, 1974; Mayer, Stiehl & Greeno, 1975). Conceptual understanding is a worthwhile goal of science teaching; but what is conceptual understanding and how is it taught? In this article we shall take a look at the models of human memory and knowledge (cognitive structures) that are associated with conceptual understanding and the ability to do transfer problems. These models will then be used to recommend specific teaching strategies.

Cognitive Structures Associated With Understanding

Studies in complex domains such as solving science problems (Bromage & Mayer, 1981; Heller & Reif, 1984; Robertson, 1986) have suggested that conceptual understanding is associated with connections -- connections between science concepts and everyday life and connections among the different science concepts in a discipline. Someone who is good at solving transfer problems does not randomly connect concepts (which might occur when using memorized algorithms to solve problems) but rather integrates the concepts into a well-structured knowledge base. Broad, organizing concepts are situated at the top of the hierarchy and useful ancillary knowledge is contained in lower levels, as Figure 1 shows for selected physics concepts. The concept map illustrated in Figure 1 is not complete, but it does clearly show the relative importance and appropriate connections among some physics concepts. For instance, the map shows that friction and electrical forces are not major problem-solving principles but merely types of forces that one might consider when using the principle of Newton's Second Law.

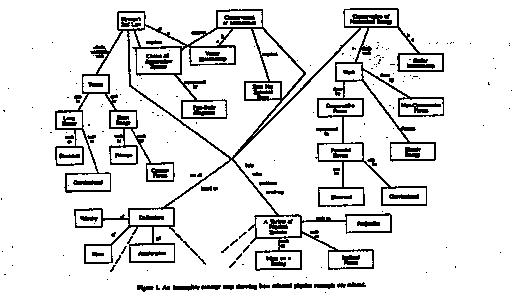
Major principles such as Conservation of Energy are at the top of the hierarchy, and physical characteristics of systems (e.g. whether a spring is present) are at the bottom, which lets the student know the relative importance of these ideas.

For the purpose of solving transfer problems, this well-structured knowledge base appears to be more important than the utilization of strategies such as setting goals and subgoals and working backwards from the goal. These strategies may be helpful, but without utilizing an accompanying "connectedness" of concepts specific to the discipline, one cannot be good at solving problems in science and other complex domains.

What to Do?

If one agrees that conceptual understanding in a discipline is desirable, then what can a teacher do about it? The following are appropriate teaching strategies suggested by research:

1) Help your students to see the structure of your discipline. Show them the "big picture" -- how concepts connect with one another and with everyday experiences. Concept Mapping (Novak & Gowin, 1984) shown in Figure 1, is an excellent tool for illustrating how concepts are related. Explicate the "ancillary knowledge" associated with formulas and principles -- this is knowledge that students use to "make sense" of a formula rather than just memorize it.

2) The most important thing you are presenting to students is the big picture, so allow them to concentrate on the big picture by making sure that they can use certain skills almost automatically. For example, one is not free to acquire a conceptual understanding of an equation such as F = ma if the use of an algebraic symbols in an equation is not second nature. Similarly, one cannot begin to concentrate on the meaning of words if one doesn't know the alphabet well. This is not to say that skills should be memorized; you should teach them in a meaningful way, just as you should teach higher-level concepts in a meaningful way. However, students should then practice the skills until they no longer present a hindrance to concentrating on more important matters.

3) Install in your students the desire to make sense of the subject matter. Encourage them to look for the connections among concepts and to structure these concepts in a hierarchy. Encourage your students to be dissatisfied with explanations that are to be memorized rather than understood. Although a well structured knowledge base in one discipline will not transfer to another discipline, perhaps the ability and desire to look for the appropriate conceptual structure in the new discipline is transferable.

4) Test your students for their ability to solve transfer problems. Testing students on problems that are exactly like ones they have done in their homework is a sure way to promote memorization of problem types. If, however, students know that the test problems will be unfamiliar, they are more likely to try to acquire the conceptual understanding necessary to do them. If you are able to help your students truly understand concepts, perhaps at some point during the year they will stop referring to the transfer problems as "trick questions!"

5) Finally, allow your students the time necessary to acquire conceptual understanding. People need time to establish connections and see how concepts fit together. Reduce the number of topics you cover in your science course. Teach fewer (important) concepts in greater depth. Allow more time in laboratory explorations that are meaningful rather than an exercise in following recipes. It is better for your students to understand a limited number of science concepts than to memorize many concepts that they are unable to apply in novel situations.

William C. Robertson is a staff associate at the Biological Sciences Curriculum Study. He is a member of NARST, an organization dedicated to improving science teaching through research.

by William C. Robertson

References

Bromage, B. K., & Mayer, R. E. (1981). Relationship between what is remembered and creative problem solving performance in science learning. Journal of Educational Psychology, 73, 451-461.

Chi, M. T. H., Feltovich, P., & Glaser, R. (1981). Categorization and representation of physics problems by experts and novices. Cognitive Science, 5, 121-152.

Heller, J. I. , & Reif, F. (1984). Prescribing effective human problem-solving processes: Problem description in physics. Cognition and Instruction, I, 177-216.

Katona, G. (1940). Organizing and memorizing.  New York: Columbia University Press.

Mayer, R. E. (1974). Acquisition processes and resilience under varying testing conditions for structurally different problem solving procedures. Journal of Educational Psychology, 66, 644-656.

Mayer, R. E., Stiehl, C. C., & Greeno, J. G. (1975). Acquisition of understanding and skill in relation to subjects' preparation and meaningfulness of instruction. Journal of Educational Psychology, 67, 331-350.

Novak, J. D., & Gowin, D. B. (1984). Learning how to learn.  New York: Cambridge University Press.

Robertson, W. C. (1986). Measurement of conceptual understanding in physics: Predicting performance on transfer problems involving Newton's second law. Doctoral dissertation, University of Colorado.

Simon, D. P., & Simon, H. A. (1978). Individual differences in solving physics problems. In Siegler, R. (Ed.), Children's thinking: What develops?   Hillsdale, NJ: Erbau.